Перейти к:
Физическое моделирование для оценки воздействия микроимпульсных режимов лазерного излучения на хориоретинальный комплекс человеческого глаза на основе теории активированного комплекса
https://doi.org/10.37895/2071-8004-2022-26-3-4-47-55
Аннотация
Цель: построить физическую модель на основе теории активированного комплекса (ТАК) с показателями ΔH и ΔS из работ Г. И. Желтова и соавторов для оценки степени воздействия микроимпульсных режимов лазерного излучения на хориоретинальный комплекс (ХРК), провести сравнение с моделями на основе интеграла Аррениуса и результатами тестирования микроимпульсного режима по данным аутофлюоресценции.
Материал и методы. Моделирование степени повреждения ХРК и прилежащих структур проводили с помощью уравнения Эйринга. Показатели ΔH = 360 000 Дж/моль и ΔS = 890 Дж/моль·град для комплекса белков и других органических структур РПЭ были определены Г. И. Желтовым с соавторами in vivo в серии лазерных экспериментов на приматах. Для моделирования применяли коэффициент поглощения 460 см–1, для длины волны 577 нм слоем РПЭ толщиной 10 мкм и пропускания 37 %. Тестирование микроимпульсного режима (50 мкс, 2,4 %, 10 мс, 100 мкм, 0,4–1,9 Вт) было проведено на навигационном лазере Navilas 577s у пациентов в возрасте 35–46 лет с 2–3-м типом внешности по шкале Фитцпатрика и оценено по данным коротковолновой аутофлюоресценции (488 нм).
Результаты. Построена физическая модель на основе ТАК с применением интеграла Эйринга. Результаты моделирования степени повреждения РПЭ от мощности совпадают с результатами тестирования микроимпульсного режима на пациентах по данным аутофлюоресценции. Уточнен средний коэффициент поглощения РПЭ равный 440 см–1 для пациентов возраста 35–46 лет и 2–3-м типом внешности по шкале Фитцпатрика.
Заключение. Компьютерное моделирование на основе ТАК с применением уравнения Эйринга с ΔH и ΔS для комплекса белков и других органических структур РПЭ, полученными в работах Г. И. Желтова, показало высокое соответствие с результатами тестирования микроимпульсного режима на реальных пациентах. Моделирование не требует подгонки каких-либо свободных параметров, в отличие от подходов, основанных на использовании уравнения Аррениуса, позволяет определять коэффициенты поглощения для узкой выборки пациентов и оценивать уровень повреждения РПЭ и прилежащих структур лазерным излучением.
Ключевые слова
Для цитирования:
Иванова Е.В., Володин П.Л. Физическое моделирование для оценки воздействия микроимпульсных режимов лазерного излучения на хориоретинальный комплекс человеческого глаза на основе теории активированного комплекса. Лазерная медицина. 2022;26(3-4):47-55. https://doi.org/10.37895/2071-8004-2022-26-3-4-47-55
For citation:
Ivanova E.V., Volodin P.L. Physical modelling to assess the effect of micropulse modes of laser radiation at the chorioretinal complex of the human eye based on the theory of activated complex. Laser Medicine. 2022;26(3-4):47-55. (In Russ.) https://doi.org/10.37895/2071-8004-2022-26-3-4-47-55
Георгий Иванович Желтов (1 июня 1939–7 ноября 2020), главный научный сотрудник Института физики НАН Беларуси, доктор физико-математических наук, лауреат Государственной премии Республики Беларусь, много лет посвятил изучению воздействия лазерного излучения на ткани глаза и определению условий его безопасного использования. С участием Георгия Ивановича были проведены многочисленные эксперименты на животных и созданы математические модели деструкции гетерогенных биоструктур, таких как сетчатка, под действием лазерного излучения, что внесло существенный вклад в развитие знаний о физических механизмах взаимодействия высокоинтенсивного лазерного излучения со структурами глаза. Результаты исследований стали основой для создания ряда принципиально новых медицинских приборов и методик лечебного воздействия на ткани высокоинтенсивного лазерного излучения. Указанные разработки обеспечили реализацию малоинвазивных методов лечения в офтальмологии. Результаты научных достижений Георгия Ивановича Желтова применяются в настоящее время и легли в основу построения компьютерной модели по изучению воздействия микроимпульсного режима на ткани глаза.
«С появлением мощной лазерной техники появились принципиально новые возможности для проведения физических исследований. Это открытие новых эффектов и явлений, связанных главным образом с высокими плотностями потоков и когерентностью электромагнитного излучения. А также изучение взаимодействия мощных световых потоков с жидкими и квазижидкими средами, включающее как объект моделирования подавляющее большинство биологических клеточных структур».
Г. И. Желтов (1996)
Современные серийные лазерные установки могут оказывать воздействие с высокой плотностью энергии на структуры хориоретинального комплекса (ХРК) в широком диапазоне мощности и времени, что открывает новые возможности по лечению заболеваний центральной области сетчатки, включая наиболее функционально-значимую фовеальную аваскулярную зону [1–3]. Для определения режимов с максимальным избирательным воздействием на ретинальный пигментный эпителий (РПЭ) при отсутствии повреждения нейросенсорной сетчатки и хориоидеи необходимо подробное физическое моделирование процессов лазерного воздействия на ХРК и проведение тестирования лазерного режима [4][5].
С учетом технических характеристик современных лазерных установок, которые применяются для лечения заболеваний глазного дна, основным механизмом повреждения тканей ХРК является термоденатурация протеинов [6][7]. Моделирование степени повреждения РПЭ и прилежащих структур с применением интеграла Аррениуса широко применяется в офтальмологии для изучения лазерного воздействия на ткани глаза [8–11]. Однако уравнение Аррениуса не следует из какой-либо физической теории, а является эмпирическим. Показатели А и ΔЕ не являются термодинамическими величинами, их значения зависят от условий проведения эксперимента и подбираются для лучшего соответствия наблюдаемым данным. Как видно из таблицы 1, значения ΔE отличаются в разы, а А – на порядки. При этом известно, что термодинамическая стабильность соединений белков практически похожа по физическим свойствам при разных мутациях в генах [12][13], то есть значение энергии активации комплекса белков близких видов не может значительно различаться.
Причиной значительной вариабельности А и ΔЕ при определении этих нормировочных величин методом подгонки (фитирования) к экспериментальным данным является большой разброс других физических показателей, используемых при построении модели глаза, например коэффициента поглощения (табл. 2). Наибольшее разнообразие наблюдается в прозрачности оптических сред и концентрации меланина в РПЭ, которая сильно варьирует в зависимости от этнических особенностей [14]. Именно уровень пропускания и поглощения лазерного излучения ХРК значительно отличается у каждого человека и напрямую зависят от таких персональных характеристик, как возраст и тип внешности [15]. Поэтому для построения точной и пригодной для практического применения физической модели воздействия лазерного излучения на ХРК человека требуется иной подход: необходимо учитывать индивидуальные свойства, а термохимические характеристики белков считать практически неизменными [16].
В современной химической кинетике для описания реакций применяется теория активированного комплекса (ТАК), из которой следует формула для коэффициента абсолютных скоростей реакций, полученная на основе уравнения Эйринга, также называемого уравнением Эйринга – Полани [17]. В уравнении Эйринга вместо показателей А и ΔЕ применяются энтропия и энтальпия или свободная энергия Гиббса. Эти величины являются обычными показателями термодинамики, физической химии и определяются по стандартизированной методологии на основании калориметрических измерений с высокой точностью. Показатели ΔH и ΔS для комплекса белков и других органических структур РПЭ были определены in vivo в серии лазерных экспериментов на приматах (rhesus macaque), проведенных Г. И. Желтовым с соавторами [1][18] и в дальнейшем уточнены по результатам применения методов моделирования в офтальмохирургии [19]. Полученные в экспериментах Желтова данные ΔH и ΔS позволяют построить модель на основе уравнения Эйринга, сравнить с результатами тестирования микроимпульсного режима по данным аутофлюоресценции, уточнить значения коэффициента поглощения для исследуемых групп пациентов.
МАТЕРИАЛ И МЕТОДЫ
ПАРАМЕТРЫ МОДЕЛИ
Для построения компьютерной модели нагрева тканей и денатурации белков использовали показатели, описанные ниже. Пропускание излучения с длиной волны 577 нм на отрезке «роговица – сетчатка», измеренное прямым методом, который применяется для оценки прохождения узкого светового пучка через структуры глаза, составляет 37 % [20]. Нейросенсорной сетчаткой поглощается 13 % излучения с длиной волны 577 нм [21][22]. Значения коэффициента поглощения, по данным литературы [22–27], имеют большой разброс, поэтому использовали центрально устойчивое медианное значение коэффициента абсорбции в 460 см–1 (табл. 2). Толщина слоя РПЭ – 10 мкм.
ОПИСАНИЕ ФИЗИЧЕСКОЙ МОДЕЛИ
Моделирование процессов нагрева и распределения тепла в ХРК путем численного решения дифференциального уравнения теплопроводности подробно описано в ранее выполненном исследовании [5]. Определение степени повреждения тканей проводилось с помощью уравнений Аррениуса (уравнение 1) и Эйринга (уравнение 4).
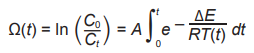 (1)
(1)
Данное уравнение называют интегралом повреждения Аррениуса, а его значение обозначают Ω, которая характеризует степень повреждения тканей и может принимать значение от 0 до ∞ (бесконечности). Точное значение омеги, определяющей порог повреждения неизвестно, но принято считать, что Ω = 1 [10]. Пары А и ΔE определены в различных экспериментах и представлены в таблице 1.
Согласно ТАК и формуле Эйринга, абсолютный коэффициент скорости определен выражением, представленным в уравнении 2:
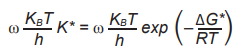 (2),
(2),
где k – постоянная Больцмана, h – постоянная Планка, T – абсолютная температура (K°),
R – универсальная газовая постоянная, ϖ – безразмерный показатель, ΔG – изменение свободной энергии Гиббса, которое в предположении о постоянстве давления определяется выражением, описанным в уравнении 3:
∆G = ∆H – T × ∆S (3),
где ΔH – изменение энтальпии (Дж/моль), ΔS – изменение энтропии (Дж/моль Ко).
Определение параметра ϖ выходит за рамки теории абсолютных скоростей. Однако для сложных реакций считается равным 1, что не противоречит экспериментальным данным [28].
ΔH = 360 000 Дж/моль и ΔS = 890 Дж/моль·град определены для комплекса белков и других органических структур РПЭ in vivo на приматах [1][18][19].
По аналогии с интегралом Аррениуса на основе уравнения скоростей реакций Эйринга выведем выражение для степени повреждения белкового комплекса ХРК в ТАК, назовем его по аналогии интегралом повреждения Эйринга (уравнение 4):
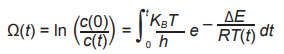 (4).
(4).
Для численного решения уравнения теплопроводности был использован размер вычислительной сетки до 3,2 × 1011 и неявный метод Рунге – Кутты второго порядка. Графики были построены с использованием программ ROOT и Microsoft Office Excel (Microsoft Corp., США).
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ВОЗДЕЙСТВИЯ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ НА ТКАНИ ХРК ДЛЯ РЕЖИМА ЕДИНИЧНОГО ИМПУЛЬСА (50 МКС) НА ОСНОВЕ ТАК С ПРИМЕНЕНИЕМ ИНТЕГРАЛА ЭЙРИНГА
Результаты моделирования оценивали по кривым эффективности, которую рассчитывали как отношение количества денатурированного белка внутри слоя РПЭ к общему количеству белка в РПЭ в зависимости от мощности импульса. Сравнение результатов моделирования одиночного импульса (50 мкс) на основе ТАК с применением уравнения Эйринга и уравнений Аррениуса для различных параметров A и ΔE представлены на рисунке 1.
Для анализа полученных результатов использовали такую меру сравнения, как эффективная доза (ED). Уровень воздействия, необходимый для достижения данного порога, обозначается как EDх, где ED – доза, необходимая для достижения повреждения в x процентов. При оценке воздействия на РПЭ, эффективность (η) отражает процент повреждения клеток РПЭ. Тогда ED50 – это доза воздействия излучения, при которой достигается 50 % повреждения РПЭ.
Как видно из таблицы 3 и графиков на рисунке 1, зависимость эффективности от мощности сильно отличается от используемых значений А и ΔЕ. Результаты моделирования 1 импульса на основе уравнения Эйринга практически совпадают с результатами моделирования Аррениуса с вариантами пар A и ΔE № 6. На уровне ЕД50 значения мощности практически не отличаются и составляют 2,2 и 2,25 Вт для модели № 7 и № 6 соответственно. Показатели А и ΔE модели № 6 были определены по результатам тестирования селективного микроимпульсного режима по данным аутофлюоресценции [5].
СРАВНЕНИЕ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ, ПРОВЕДЕННОГО С ПРИМЕНЕНИЕМ ИНТЕГРАЛОВ АРРЕНИУСА И ЭЙРИНГА, С РЕЗУЛЬТАТАМИ ТЕСТИРОВАНИЯ СЕЛЕКТИВНОГО МИКРОИМПУЛЬСНОГО РЕЖИМА (50 МКС, 2,4 %, 10 МС, 100 МКМ) ПО ДАННЫМ АУТОФЛЮОРЕСЦЕНЦИИ
Коротковолновая аутофлюоресценция (488 нм) является самым чувствительным методом диагностики повреждения РПЭ лазерным излучением в микроимпульсном режиме [29]. Тестирование селективного микроимпульсного режима (50 мкс, 2,4 %, 10 мс, 100 мкм, 0,4–1,9 Вт) было проведено на навигационной лазерной установке Navilas 577s на узкой выборке пациентов в возрасте 35–46 лет с 2–3-м типом внешности по шкале Фитцпатрика, оценено по данным аутофлюоресценции и подробно описано в статье [5].
Участки лазерного воздействия на снимках аутофлюоресценции определяются как гипофлюоресцентные пятна [5][30]. Вероятность визуализации пятна (ВВП) в зависимости от мощности излучения представлена на рисунке 2. С помощью метода максимизации правдоподобия была получена логистическая функция (уравнение 5), описывающая ВВП после лазерного воздействия по данным аутофлюоресценции от мощности. Значение χ 2 равно 12,5, при количестве степеней свободы 14. Поэтому функция ВВП (уравнение 5) может быть использована для описания результатов тестирования (ВВП) в зависимости от мощности лазера для данного режима.
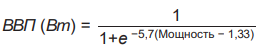 (5)
(5)
На рисунке 3 приведены результаты компьютерного моделирования микроимпульсного режима (50 мкс, 2,4 %, 10 мс, 100 мкм) с применением интеграла Аррениуса (с различными парами А и ΔЕ) и интегралом Эйринга, а также наложена функция ВВП (мощность), описывающая результаты тестирования микроимпульсного режима по данным аутофлюоресценции.
Как продемонстрировано на графике, моделирование эффективности от мощности, построенное с помощью интеграла Эйринга, практически совпадает с результатами тестирования селективного микроимпульсного режима по данным аутофлюоресценции без какой-либо дополнительной подгонки параметров. Таким образом, уравнение Эйринга может напрямую применяться для моделирования селективного микроимпульсного режима, не требуя при этом подбора А и ΔЕ.
Однако, как видно из рисунка 3, совпадение эффективности, полученной на основе уравнения Эйринга, с логистической функцией ВВП (мощность) хорошее, но не полное. При моделировании с применением интеграла Аррениуса для лучшего совпадения и описания экспериментальных данных подбирают А и ΔЕ [10][11], а при моделировании на основе ТАК значения ΔН и ΔS фиксированы. Свободным (вариабельным) параметром модели является коэффициент поглощения. Как видно, при изменении коэффициента поглощения в допустимом диапазоне, согласно данным литературы (табл. 2), происходит изменение функции эффективности (рис. 4). Поэтому, меняя коэффициент поглощения, можно подобрать соответствующую функцию эффективности, при которой наблюдается наилучшее совпадение с данными тестирования.
При значении коэффициента поглощения 440 см–1 моделирование эффективности, проведенное с помощью уравнения Эйринга, наилучшим образом описывает результаты тестирования селективного микроимпульсного режима по данным аутофлюоресценции на узкой выборке пациентов в возрасте 35–46 лет и 2–3-м типом внешности по шкале Фитцпатрика (рис. 5).
Таким образом, проведение моделирования на основе ТАК с применением уравнения Эйринга позволяет уточнить значение коэффициента поглощения исследуемой выборки.
Одной из проблем физической модели является количество неопределенных параметров. Применение уравнения Эйринга избавляет от подбора показателей А и ΔЕ, которые имеют большой разброс значений, так как отражают не термохимические свойства белков, а все особенности эксперимента. Процессы необратимой тепловой денатурации комплекса белков, которые связаны с разрушением первичной структуры практически не зависят от генетического многообразия популяции [12][13]. Поэтому моделирование на основе ТАК с полученными в экспериментах на приматах ΔH и ΔS для комплекса белков и других органических структур РПЭ для расчета интеграла повреждения становится более стабильным, физически корректным и точным. При сравнительном анализе результаты компьютерного моделирования на основе ТАК практически совпадают с результатами моделирования классическим методом с применением интеграла Аррениуса с показателями A = 1,6 × 10 55 c–1, ΔE = 3,34 × 10 5 Дж/моль, которые получены на результатах тестирования микроимпульсного режима на пациентах по данным аутофлюоресценции. Поэтому модель на основе ТАК предпочтительно использовать для оценки повреждения РПЭ и прилежащих структур лазерным излучением.
Таблица 1
Значения А и ΔE из различных литературных источников, в которых изучали повреждение структур глаза лазерным излучением с применением уравнения Аррениуса
Table 1
Values A and ΔE taken from various literary sources, in which damage to eye structures with laser radiation were studied using the Arrhenius equation
№ | A – фактор частоты A – frequency factor | ΔE – энергия активации ΔE – activation energy | Ссылки на источники литературы References |
1 | 3 × 10 44 с–1 | 2,73 × 10 5 Дж/моль | 10 |
2 | 1,6 × 10 55 с–1 | 3,4 × 10 5 Дж/моль | 11 |
3 | 3,1 × 10 99 с–1 | 6,28 × 10 5 Дж/моль | 9 |
4 | 1044 с–1 | 2,93 × 10 5 Дж/моль | 8 |
5 | 4,3 × 10 64 с–1 | 4,2 × 10 5 Дж/моль | 8 |
6 | 1,6 × 10 55 с–1 | 3,34 × 10 5 Дж/моль | 5 |
Таблица 2
Значения коэффициента поглощения лазерного излучения (577 нм) слоем РПЭ толщиной 10 мкм (представлены данные, найденные в литературе)
Table 2
Coefficient values of laser radiation (wavelength 577 nm) after absorption with RPE 10 μm thick tissue layer
(data from literature are presented)
Концентрация меланина, ммоль/л Melanin concentration, mmol/l | Процент поглощения, % Absorption percentage, % | Коэффициент поглощения, см–1 Absorption coefficient, cm–1 | Ссылки на публикации References |
| 65 | 990 | 22 |
|
| 720 | 24 |
~300 |
| 570 | 27 |
242 |
| 460 | 25 |
| 25–55 | 450 | 14 |
60–100 |
| ~150 | 23 |
63 |
| 120 | 26 |
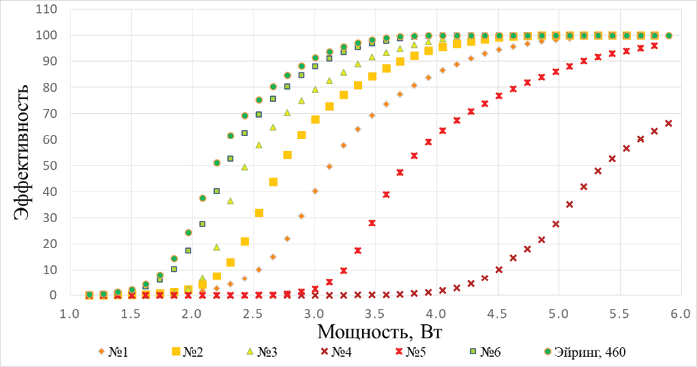
Рис. 1. Зависимости эффективности от мощности, рассчитанные для значений A и ΔE из таблицы 1 с помощью интеграла Аррениуса (№ 1–6) и уравнения Эйринга
Fig. 1. Dependences of efficiency on power calculated for values A and ΔE in Table 1 using Arrhenius integral (N 1–6) and Eyring equation
Таблица 3
Значение пороговой мощности для разных вариантов пар значений А и ΔE уравнений Аррениуса и Эйринга
Table 3
Threshold power indicators for different variants of pairs of values A and ΔE of Arrhenius and Eyring equations
1 имп., 50 мкс 1 impulse, 50 µs | № 1 No. 1 | № 2 No. 2 | № 3 No. 3 | № 4 No. 4 | № 5 No. 5 | № 6 No. 5 | Эйринг, 460 Eyring, 460 |
ED50 | 3,1 | 2,75 | 2,45 | 5,35 | 3,75 | 2,25 | 2,2 |
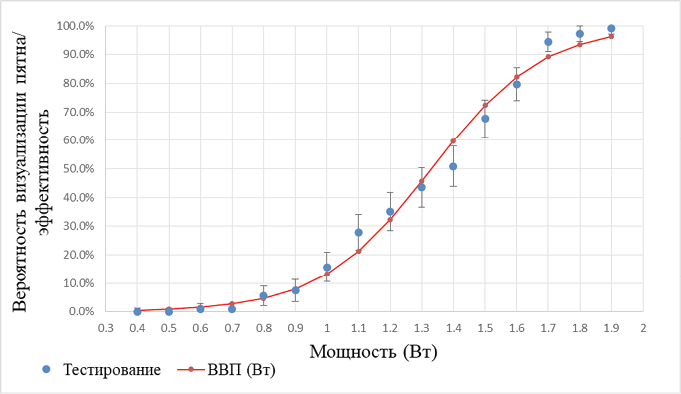
Рис. 2. Логистическая функция ВВП от мощности, полученная на основе результатов тестирования микроимпульсного режима [5]
Fig. 2. Logistic function of probability of spot visualization depending on power, obtained after testing of micropulse mode
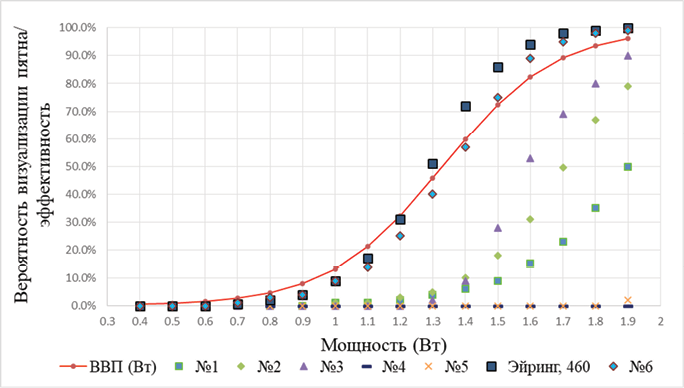
Рис. 3. Сравнение функций эффективности, построенных с применением различных пар А и ΔЕ интеграла Аррениуса и Эйринга, с результатами тестирования микроимпульсного режима
Fig. 3. Comparison of efficiency functions constructed using various pairs of A and ΔЕ of Arrhenius and Eyring integral with results of testing of micropulse mode
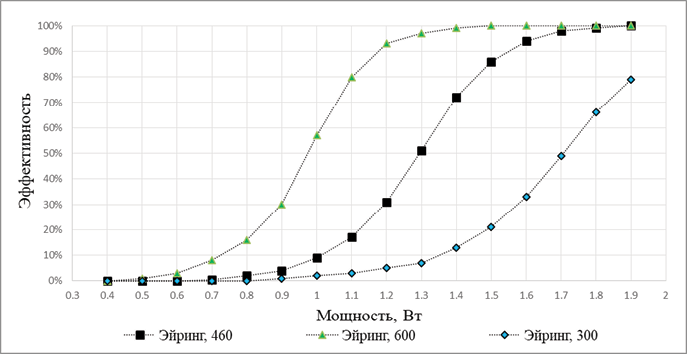
Рис. 4. Изменение функций эффективности от мощности, полученных моделированием с применением интеграла Эйринга при различных коэффициентах поглощения
Fig. 4. Changes in efficiency functions depending on power obtained by modeling using the Eyring integral in different absorption coefficients
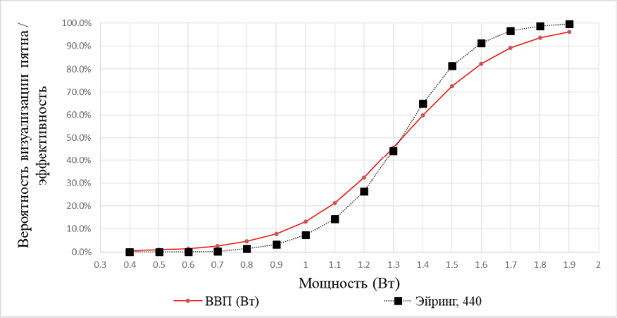
Рис. 5. Сравнение эффективности, полученной моделированием уравнения Эйринга с коэффициентом поглощения 440 см–1, с логистической функцией ВВП (мощность)
Fig. 5. Comparison of the efficiency obtained by modeling of Eyring equation and absorption coefficient 440 cm-1 with the logistic function of probability of spot visualization (power)
ВЫВОДЫ
- Построена физически корректная модель на основе теории активированных комплексов с показателями ΔHи ΔS для комплекса белков и других органических структур РПЭ, определенных Г. И. Желтовым и соавторами, которая позволяет оценивать уровень повреждения ХРК человека микроимпульсным режимом лазерного излучения.
- Результаты полученной модели совпадают с результатами тестирования микроимпульсного режима по данным коротковолновой аутофлюоресценции, проведенного на пациентах европейского типа внешности.
- С помощью полученной модели и результатов тестирования микроимпульсного режима был уточнен средний коэффициент поглощения РПЭ выборки пациентов возраста 35–46 лет и 2–3-м типом внешности по шкале Фитцпатрика, значение которого составило 440 см–1.
- Полученная модель рекомендована к применению для моделирования воздействия лазерного излучения на ХРК.
Список литературы
1. Желтов Г.И. Воздействие интенсивного оптического излучения на ткани глаз: исследования и приложения: диссертация ... д-ра мед. наук. Минск; 1996.
2. Желтов Г.И. Биофизика деструктивного действия надпорогового лазерного излучения на ткани глазного дна. II Всероссийский семинар «МАКУЛА 2006»: материалы научнопрактической конференции. Ростов н/Д.; 2006: 71–85.
3. Тахчиди Х.П., Качалина Г.Ф., Желтов Г.И., Иванова Е.В. Новая технология восстановления зрительных функций, основанная на избирательном воздействии коротких импульсов лазерного излучения на пигментный эпителий сетчатки. Офтальмология в Беларуси. 2010; 4 (7): 79–83.
4. Качалина Г.Ф., Желтов Г.И., Иванова Е.В. Оптимизация режимов лазера IRIS Medical IQ 577 для избирательного воздействия на пигментный эпителий сетчатки. Офтальмология Восточная Европа. 2015; 4 (27): 69–77.
5. Ivanova E.V., Volodin P.L., Guskov A.V. Determination of micropulse modes with targeted damage to the retinal pigment epithelium using computer modeling for the development of selective individual micropulse retinal therapy. Curr Eye Res. 2022; 47 (1): 107–114. DOI: 10.1080/02713683.2021.1 962360
6. Schuele G., Rumohr M., Huettmann G., Brinkmann R. RPE damage thresholds and mechanisms for laser exposure in the microsecond-to-millisecond time regimen. Invest Ophthalmol Vis Sci. 2005; 46 (2): 714–719. DOI: 10.1167/iovs.040136
7. Alt C., Pitsillides C.M., Roegener J., Lin C.P. Monitoring intracellular cavitation during selective targeting the retinal pigment epithelium. Proc SPIE. 2003; 4951: 48–55. DOI: 10.1117/12.477956
8. Banerjee R.K., Zhu L., Gopalakrishnan P., Kazmierczak M.J. Influence of laser parameters on selective retinal treatment using single-phase heat transfer analyses. Med Phys. 2007; 34 (5): 1828–1841. DOI: 10.1118/1.2718731
9. Denton M.L., Clark C.D., Foltz M.S., et al. In-vitro retinal model reveals a sharp transition between laser damage mechanisms. J Biomedical Optics. 2010; 15 (3): 030512. DOI: 10.1117/1.3449107
10. Schlott K., Koinzer S., Ptaszynski L., et al. Automatic temperature controlled retinal photocoagulation. J Biomed Opt. 2012; 17 (6): 061223. DOI: 10.1117/1.JBO.17.6.061223
11. Wang J., Quan Y., Dalal R., Palanker D. Comparison of continuous-wave and micropulse modulation in retinal laser therapy. Invest Ophthalmol Vis Sci. 2017; 58 (11): 4722–4732. DOI: 10.1167/iovs.17-21610
12. Sanchez-Ruiz J.M. Protein kinetic stability. Biophys Chem. 2010; 148 (1–3): 1–15. DOI: 10.1016/j.bpc.2010.02.004
13. Godoy-Ruiz R., Ariza F., Rodriguez-Larrea D., et al. Natural selection for kinetic stability is a likely origin of correlations between mutational effects on protein energetics and frequencies of amino acid occurrences in sequence alignments. J Mol Biol. 2006; 362 (5): 966–978. DOI: 10.1016/j.jmb.2006.07.065
14. Geeraets W, Williams R, Chan G, et al. The relative absorption of thermal energy in retina and choroid. Invest Ophthalmol Vis Sci. 1962; 1: 340–347.
15. Ivanova E.V., Volodin P.L. Development of the selective micropulse individual retinal therapy depends on age and type on the Fitzpatrick scale. Graefes Arch Clin Exp Ophthalmol. 2022; 261 (2): 381–390. DOI: 10.1007/s00417-022-05800-9
16. Preece S.J., Claridge E. Monte Carlo modelling of the spectral reflectance of the human eye. Phys Med Biol. 2002; 47 (16): 2863–2877. DOI: 10.1088/0031-9155/47/16/303
17. Eyring H. The activated complex in chemical reactions. J Chem Phys. 1935; 3 (2): 107–115. DOI: 10.1063/1.1749604
18. Гапеева Т.А., Глазков В.Н., Подольцев А.С. и др. Лазерный метод определения температурной зависимости константы скорости реакции фотокоагуляции in vivo. Весцi АН БССР. Серыя фiзiка-матэматычных навук. 1986; 3: 81–85.
19. Федоров С.Н., Ивашина А.И., Антонова Е.Г. и др. Математическое моделирование термохимических процессов при термокоагуляции. Офтальмохирургия. 1992; 3: 8–13.
20. Boettner E.A., Walter J.R. Transmission of the ocular media. Invest Ophthalmol Vis Sci. 1962; 1: 776–783.
21. Guo Y., Yao G., Lei B., Tan J. Monte Carlo model for studying the effects of melanin concentrations on retina light absorption. J Opt Soc Am A Opt Image Sci Vis. 2008; 25 (2): 304–311. DOI: 10.1364/josaa.25.000304
22. Hammer M., Roggd A., Schweitzert D., Muller G. Optical properties of ocular fundus tissues – an in vitro study using the double-integrating-sphere technique and inverse Monte Carlo simulation. Phys Med Biol. 1995; 40 (6): 963–978. DOI: 10.1088/0031-9155/40/6/001
23. Durairaj C., Chastain J.E., Kompella U.B. Intraocular distribution of melanin in human, monkey, rabbit, minipig and dog eyes. Exp Eye Res. 2012; 98 (1): 23–27. DOI: 10.1016/j. exer.2012.03.004
24. Geeraets W.J., Berry E.R. Ocular spectral characteristics as related to hazards from lasers and other light sources. Am J Ophthalmol. 1968; 66 (1): 15–20. DOI: 10.1016/00029394(68)91780-7
25. Schmidt S.Y., Peisch R.D. Melanin concentration in normal human retinal pigment epithelium. Regional variation and age-related reduction. Invest Ophthalmol Vis Sci. 1986; 27 (7): 1063–1067.
26. Shu X., Li H., Dong B., et al. Quantifying melanin concentration in retinal pigment epithelium using broadband photoacoustic microscopy. Biomed Opt Express. 2017; 8 (6): 2851–2865. DOI: 10.1364/BOE.8.002851
27. Shu X., Liu W., Zhang H.F. Monte Carlo investigation on quantifying the retinal pigment epithelium melanin concentration by photoacoustic ophthalmoscopy. J Biomed Opt. 2015; 20 (10): 106005. DOI: 10.1117/1.JBO.20.10.106005
28. Картель Н.Т., Лобанов В.В. Теория активированного комплекса. Кн. 1. Физика поверхности. Киев: Институт химии поверхности НАН Украины; ООО “Интерсервис”; 2015; 1 (9): 363–389.
29. Володин П.Л., Иванова Е.В., Соломин В.А. Возможности современных методов диагностики и компьютерной обработки данных с помощью программы «Фемтоскан» для выявления слабых термических повреждений клеток ретинального пигментного эпителия. Лазерная медицина. 2018; 22 (1): 52–56. DOI: 10.37895/2071-8004-2018-22-152-56
30. Framme C., Schüle G., Brinkmann R., et al. Fundus autofluorescence after selective RPE laser treatment. Ophthalmologe. 2002; 99 (11): 854–860. DOI: 10.1007/ s00347-002-0684-z
Об авторах
Е. В. ИвановаРоссия
Иванова Елена Владимировна – кандидат медицинских наук, врач-офтальмолог отделения лазерной хирургии сетчатки
Москва
П. Л. Володин
Россия
Володин Павел Львович – доктор медицинских наук, заведующий отделом лазерной хирургии сетчатки
Москва
Рецензия
Для цитирования:
Иванова Е.В., Володин П.Л. Физическое моделирование для оценки воздействия микроимпульсных режимов лазерного излучения на хориоретинальный комплекс человеческого глаза на основе теории активированного комплекса. Лазерная медицина. 2022;26(3-4):47-55. https://doi.org/10.37895/2071-8004-2022-26-3-4-47-55
For citation:
Ivanova E.V., Volodin P.L. Physical modelling to assess the effect of micropulse modes of laser radiation at the chorioretinal complex of the human eye based on the theory of activated complex. Laser Medicine. 2022;26(3-4):47-55. (In Russ.) https://doi.org/10.37895/2071-8004-2022-26-3-4-47-55
JATS XML


























