Перейти к:
Методические замечания о физических параметрах низкоинтенсивного лазерного воздействия. Часть 1. Глубина проникновения лазерного излучения
https://doi.org/10.37895/2071-8004-2023-27-4-8-15
Аннотация
Цель. Общая цель данной методической статьи, состоящей из двух частей, – дать объединяющий теоретический подход к дискутируемым до сих пор проблемам определения глубины проникновения лазерного излучения в ткани и дозы лазерного терапевтического воздействия с позиций современной медицинской физики. Целью первой части статьи является обсуждение вопроса глубины проникновения лазерного излучения в ткани и органы при диагностических и лечебных процедурах и формулировка практических рекомендаций по ее оценке.
Материалы и методы. Проведен обзор современного состояния с терминами и определениями, касающимися вопросов глубины проникновения лазерного излучения. На основе разных приближений известного в физике уравнения переноса излучения приведены численные теоретические оценки глубины проникновения излучения разных длин волн в кожу для разных подходов. Методом Монте-Карло смоделирован объем мягких тканей, в котором поглощается до 95 % энергии излучения. Оценена глубина проникновения излучения исходя из линейных размеров этого объема.
Результаты. Классическая теоретическая глубина проникновения лазерного излучения в ткани и органы оказывается сильно зависящей не только от длины волны и оптических свойств тканей, но и от выбранного приближения и метода расчета. Глубина проникновения, оцененная на основе расчета объема, в котором поглощается до 95 % энергии лазерного излучения, оказывается в общем случае примерно в 3 раза больше величины классической теоретической глубины проникновения, что лучше соответствует известным экспериментальным данным.
Заключение. Глубина проникновения лазерного излучения более аргументированно в практическом плане для лечебных и диагностических процедур может определяться через эффективный облучаемый объем тканей.
Ключевые слова
Для цитирования:
Рогаткин Д.А., Тарасов А.П., Штыфлюк М.Е. Методические замечания о физических параметрах низкоинтенсивного лазерного воздействия. Часть 1. Глубина проникновения лазерного излучения. Лазерная медицина. 2023;27(4):8-15. https://doi.org/10.37895/2071-8004-2023-27-4-8-15
For citation:
Rogatkin D.A., Tarasov A.P., Shtyflyuk M.E. Methodological notes on physical parameters of low-level laser irradiation. Part 1. Penetration depth of laser light. Laser Medicine. 2023;27(4):8-15. (In Russ.) https://doi.org/10.37895/2071-8004-2023-27-4-8-15
ВВЕДЕНИЕ
Несмотря на современный уровень развития медицинской физики и достаточно длительную уже историю развития лазерных методов лечения и диагностики в медицине, вопросы глубины проникновения лазерного излучения (ЛИ) в ткани и органы, равно как и вопросы дозы лазерного лечебного воздействия, до сих пор остаются предметом споров и недостаточного понимания не только со стороны врачей, но и специалистов физико-технического профиля [1][2]. Прежде всего это касается вопросов терапевтического применения ЛИ (низкоинтенсивная лазерная терапия (НИЛТ), фотодинамическая терапия (ФДТ) и др.) и вопросов глубины или объема зондирования живых тканей оптическим излучением, не обязательно лазерным, на разных длинах волн при диагностических процедурах. К таковым относятся разные технологии оптической флоуметрии, тканевой оксиметрии, фотоплетизмографии, лазерного спектрального анализа и т. д. Как глубоко ЛИ проникает в ткани? Однажды авторам этих строк пришлось столкнуться с утверждением одного зарубежного рецензента их статьи, что поскольку глубина проникновения зеленого света в кожу, по данным литературы, не больше 1 мм, эффективная оптическая диагностика микрососудистого русла в зеленом свете невозможна. Пришлось его долго убеждать в обратном (см. далее).
А уж сколько копий было сломано в последние десятилетия в нашей стране в спорах об определении понятия дозы лазерного терапевтического воздействия — и не сосчитать [3–8 и др.]. Нужно ли определять дозу как величину с размерностью мВт/см², или мДж/см², или просто как энергию (Дж)? А может, ее надо определять через объемную плотность энергии в тканях (Дж/см³) или как поглощенную энергию на единицу массы ткани, как это и принято сегодня в классической клинической дозиметрии, т. е. как величину с размерностью Дж/кг (мДж/г)? Какую величину правильно и корректно обозначать термином «доза» в лазерной терапии? Эквивалентно ли воздействие в случае маленькой плотности мощности и длительного времени облучения и большой плотности мощности и короткого по времени облучения, если формально величины с размерностью мДж/см² будут численно равны в обоих случаях? Некоторые авторы предлагали в свое время сомнительные термины типа «поверхностное дозирование по поглощенной дозе» (т. е. сразу два каких-то «дозирования») [7] или «энергетическая плотность» [8] (нестандартный термин), чтобы как-то сгладить ситуацию.
И совсем темным пятном остается доза лазерного воздействия при облучении с помощью оптического волокна, например при внутривенном лазерном облучении крови (ВЛОК). Если при обычной чрескожной НИЛТ поверхностные плотности мощности ЛИ соответствуют диапазону 0,1–100 мВт/см² [6], то при ВЛОК с оптическим волокном диаметром 100 мкм и мощностью ЛИ на выходе из волокна 1–10 мВт подводимая плотность мощности (доза?) оказывается в диапазоне 10⁴–10⁵ мВт/см², т. е. на 2–3 порядка выше [9][10]. И без того в разных практических руководствах еще с конца 1990-х годов рекомендуемые значения «доз» у разных авторов различаются в сотни и более раз — от 0,1 до 120 Дж/см² [10]. А тут уже различия в тысячи раз… И это притом что существенного нагрева, карбонизации, выпаривания тканей при таком воздействии (т. е. их повреждения) не происходит. Это тоже требует объяснений.
Неясность во всех этих вопросах и послужила поводом для данных методических заметок. Их цель — в методическом плане с позиций медицинской физики расставить все основные точки над “i” в этих вопросах и показать, с одной стороны, возможный единый взгляд на проблему, а с другой — глубинную фундаментальную взаимосвязь разных подходов к проблеме. В частности, вопросы дозы и глубины проникновения, на первый взгляд, кажутся близкими, но не жестко взаимосвязанными. Родственными кажутся вопросы сравнения доз ЛИ при импульсном и непрерывном облучении [1][7][8], но прямо не связанными с проблемой глубины проникновения. Однако фактически, как показано в данной статье, это одна и та же методологическая проблема, просто плохо пока раскрытая (на взгляд авторов) в предыдущих публикациях.
ПОНЯТИЕ ГЛУБИНЫ ПРОНИКНОВЕНИЯ
В литературе известно много поясняющих глубину проникновения ЛИ в кожу картинок со стрелочками разной длины, направленными вглубь кожи, и разного цвета, которые обозначают разную длину волн излучения λ (например, см. в [11]). Но эти картинки дают лишь качественное представление. Поскольку речь идет о физическом факторе воздействия — электромагнитном излучении — и о физике распространения ЛИ в тканях и средах организма, то необходимо прежде всего оперировать строгой количественной физической терминологией.
Понятие глубины проникновения (толщины скин-слоя) формулируется в оптике, фотометрии и теории электромагнетизма на основе закона экспоненциального затухания Бугера [12][13]. Если представить плоскую электромагнитную волну (параллельный пучок лучей света) с плотностью мощности в сечении луча P0 [мВт/см²], которая падает на сплошную однородную материальную среду (рис. 1), обладающую коэффициентом поглощения излучения этой длины волны μа [см-¹], то по мере распространения ЛИ в этой среде с толщиной z [см] плотность мощности в луче P(z) с глубиной будет уменьшаться по экспоненте (отражением на границе среды здесь и далее для простоты пренебрегаем). Это описывается известным уравнением Бугера:
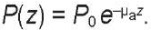 (1)
(1)
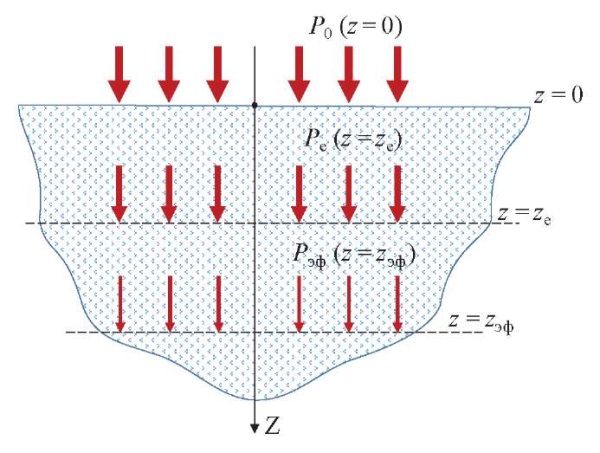
Рис. 1. Ослабление мощности параллельного пучка лучей света в поглощающей среде
Fig. 1. Power attenuation of the parallel beam of light rays in the absorbing medium
При z = zе = 1/μа поток излучения ослабнет в е раз (примерно в 2,7 раза), и эта глубина zе чисто условно в физике, подчеркиваем: условно называется глубиной проникновения излучения в среду (толщиной скин-слоя) [13]. Врачи же часто ошибочно этот термин «глубины» понимают буквально. На этой глубине, если пренебречь отражением от внешней границы, первоначальный поток, скажем, в 10 мВт/см² станет равным 3,7 мВт/см². Еще через такое же расстояние этот поток ослабнет до 1,4 мВт/см² и т. д. Но это все равно не будет нулевой поток (P (z) ≠ 0), и он может потенциально оказывать какое-то эффективное биологическое действие даже на глубине zэф, существенно большей ze, если оставшейся мощности ЛИ достаточно для такого действия.
Например, для зеленого диапазона спектра (λ = 520–550 нм) и для нормальной кровенаполненной кожи, согласно данным литературы, эффективное (усредненное по эпидермису-дерме) значение коэффициента поглощения μа в зависимости от кровенаполнения дермы и содержания меланина в эпидермисе составляет 2–10 см–¹ [14][15], что по (1) дает ze = 1–5 мм. Однако уравнение (1) и само понятие толщины скин-слоя формулируются в классической физике только для сплошной, гомогенной и поглощающей свет среды без внутренних неоднородностей. Биологические же ткани, как известно, сильно оптически неоднородны (и на уровне тканевых слоев, и на уровне отдельных клеток и их органелл), что приводит к сильному рассеянию света и существенному усложнению теоретического описания его распространения в среде. В самом общем случае этот процесс описывается либо с позиций электромагнетизма уравнениями Максвелла, либо, при рассмотрении более простых фотометрических задач, скалярным уравнением переноса излучения (УПИ). Общих точных решений УПИ для светорассеивающей среды пока не найдено, поэтому расчеты ведутся в рамках разных упрощающих аппроксимаций (приближений) – потоковых моделей Кубелки – Мунка, приближения однократного рассеяния, диффузионного приближения и т. п. [16–18]. В этих фотометрических теориях рассеяние характеризуется отдельным коэффициентом рассеяния μs [см–¹] и фазовой функцией рассеяния g, описывающей угловое распределение рассеяния в пространстве (оно может быть разным в разных направлениях). Часто вместо фазовой функции для расчетов достаточно просто среднего косинуса угла рассеяния g, тогда фазовая функция не используется.
Все это усложняет расчет и делает более сложным вид показателя экспоненты в законе затухания. Например, по глубине поток затухает в рамках приближения однократного рассеяния в соответствии с экспонентой [17]:
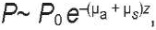 (2)
(2)
в классической 2-потоковой модели Кубелки – Мунка по экспоненте [16]:
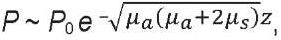 (3)
(3)
а в рамках диффузионного приближения [18]
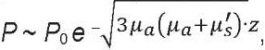 (4)
(4)
где μs′ = μs (1 − g).
По определению при таких законах затухания глубина проникновения определяется как величина, обратно пропорциональная множителю перед z в показателе экспоненты. Если взять оптические параметры кожи для зеленого света с λ = 525 нм в виде типового набора значений: μa = 5 см-¹, μs = 250 см–¹, g = 0,8 [19][20], то в первом случае (однократное рассеяние) при указанных параметрах ze = 0,04 мм, во втором случае (модель Кубелки – Мунка) ze = 0,19 мм, а в третьем (диффузионное приближение) – ze = 0,35 мм. Как видим, рассеяние еще сильнее уменьшает глубину ze в несколько раз. В приближении однократного рассеяния это уменьшение больше, а для многократного рассеяния – меньше. Многократное рассеяние определенным образом «просветляет» среду по сравнению с однократным. Но это уже детали. На такую маленькую расчетную глубину проникновения, меньше миллиметра при λ = 525 нм, и упирал наш заморский рецензент. Пришлось послать ему фотографию с мочкой уха и зеленым светодиодом, где отчетливо видно, как зеленый свет λ = 525 нм проходит сквозь мочку уха толщиной более 5 мм (рис. 2)1.
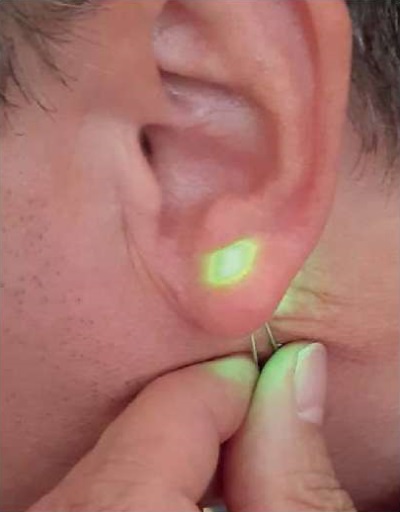
Рис. 2. Прохождение зеленого света светодиода через мочку уха толщиной 5–6 мм
Fig. 2. Passage of green LED light through the earlobe 5–6 mm thick
Как видим на рис. 2, свет проникает в ткани намного глубже теоретической «глубины проникновения». Сравнительные данные по для разных приближений и длин волн даны в таблице.
Таблица
Сравнительные данные по ze для разных приближений и длин волн
Table
Comparative data on ze for different approximations and wavelengths
Длина волны λ, нм | Оптические свойства | Глубина проникновения согласно формуле, мм: | |||
(1) | (2) | (3) | (4) | ||
315 (УФ) | μa = 60 см-¹, μs = 400 см-¹, g = 0,7 | 0,17 | 0,02 | 0,04 | 0,05 |
525 (зеленый) | μa = 5 см-¹, μs = 250 см-¹, g = 0,8 | 2,0 | 0,04 | 0,19 | 0,35 |
633 (красный) | μa = 2 см-¹, μs = 170 см-¹, g = 0,8 | 5,0 | 0,06 | 0,38 | 0,68 |
810 (ИК) | μa = 1,5 см-¹, μs = 120 см-¹, g = 0,8 | 6,7 | 0,08 | 0,52 | 0,93 |
Приведенное описание, хоть и строгое с физико-математической точки зрения, представляется мало информативным для клиники и явно занижает реальную глубину проникновения. Для клиницистов же важно знать: какая доля ЛИ окажется на той или иной глубине в реальном органе? До какой глубины доходит столько мощности (энергии) ЛИ, сколько достаточно, чтобы оказать нужное терапевтическое действие или извлечь искомую диагностическую информацию? Диагностика и лечение – это разные задачи при такой постановке вопроса.
Для целей диагностики ЛИ должно в нужном количестве либо пройти насквозь орган, чтобы быть зарегистрированным фотоприемником с его обратной стороны, например как в датчике пульсоксиметра («прищепка» на палец), либо проникнуть вглубь тканей и выйти за счет рассеяния назад в нужном количестве на освещаемую поверхность, где тоже может располагаться фотоприемник, например оптическое волокно. В первом случае (в проходящем свете) вопрос о глубине проникновения излучения не стоит – просвечивается насквозь весь орган (палец). А вот во втором случае определить, до какой глубины доходило ЛИ и с какой максимальной глубины мы получили информацию, не так просто. Навскидку даже сложно сказать, будет ли это глубина ze, или zэф, или какая-то другая, поскольку не указан критерий, как судить о такой глубине.
В свое время вопрос о таком критерии был рассмотрен в [22]. Было введено понятие «эффективный диагностический объем» (ЭДО) – такой объем ткани, который вносит в регистрируемый оптический сигнал вклад по мощности излучения, например не менее 95 % общего регистрируемого сигнала. То есть это такой объем и, соответственно, глубина zd, с которых до фотоприемника доходит не менее 95 % от общей мощности излучения, которую он регистрирует в каждом конкретном случае. Это определение позволяет численно оценивать достигаемый при реальных измерениях ЭДО.
В качестве иллюстрации рассмотрим простейшую задачу одномерного распространения света в светорассеивающей биоткани. Формулировка задачи такова: найти такую эффективную глубину зондирования zd среды распространения излучения с заданными оптическими свойствами, с которой обратнорассеянное излучение Pbs(zd), регистрируемое диагностическим прибором на поверхности этой среды в области освещения, составляет по мощности долю 0,95 от общей мощности обратнорассеянного излучения Pbs(z → ∞), которое теоретически может быть зарегистрировано от бесконечной по толщине среды. Это обратнорассеянное излучение для модельной полубесконечной среды описывается, например, в рамках классической 2-потоковой модели Кубелки – Мунка соотношением:
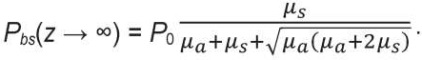 (5)
(5)
Чуть более сложное уравнение можно получить и для среды конечной толщины. Поскольку, за исключением нескольких частных случаев (мочка уха, палец), в медицине облучаются толстые слои тканей и органы и свет сквозь них практически не проходит, они могут быть приняты в модельной расчетной задаче как среды полубесконечной толщины, и для них справедливо уравнение (5). Тогда обратнорассеянное излучение Pbs(zd), выходящее из глубины zd, будет меньше Pbs(z → ∞). Соответственно, можно вычислить такую zd, с которой доходит до фотоприемника 95 % от Pbs(z → ∞), т. е.:
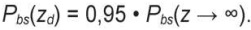 (6)
(6)
Как показано в [22], для непоглощающей свет биоткани (μа = 0)
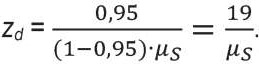 (7)
(7)
Для типовых значений μs = 20…100 см-¹ глубина зондирования zd такой биоткани в режиме обратного рассеяния оценивается в 1–10 мм. В этой же статье приведено выражение и графики для оценки zd в общем случае, когда μа ≠ 0. Показано, что типовые значения глубины зондирования тканей светом zd лежат уже в диапазоне 1–8 мм, т. е. они существенно больше оценок таблицы.
При лечебном применении ЛИ у нас сегодня нет инструментов и теорий, чтобы определить, какая доля из дошедшего до глубины z излучения окажет терапевтический эффект. С точки зрения медицинской физики лечебный эффект оказывает только энергия поглощенного излучения (различные информационные и другие аналогичные околонаучные теории здесь не рассматриваем), т. к. вызывает последовательный каскад разных фотофизических, фотохимических и фотобиологических реакций в клетках, тканях и органах [23]. Как указано в цитируемой статье, в лазерной терапии, по данным многих авторов, очень ярко проявляется зависимость «доза–эффект», поэтому понятие дозы ЛИ – одно из ключевых в методическом плане, особенно при ФДТ и ультрафиолетовой (УФ) терапии в дерматологии. Если до глубины z дойдет и поглотится там недостаточно мощности (энергии) ЛИ в единицу времени, чтобы вызвать фотофизические и фотохимические реакции, лечебного эффекта и не будет [2]. Однако в [1] правильно отмечается, что и поглотившись, скорее всего, не вся энергия света уходит на полезное лечебное действие. Например, часть квантов света, поглощенная биомолекулами, далее снова переизлучается в виде излучения флюоресценции и/или фосфоресценции (лазер-индуцированная люминесценция) [3]. Поэтому вопрос о «минимальной лечебной дозе» ЛИ правомерен и актуален до сих пор. Но он пока недостаточно изучен. Однако сейчас нам важно осознать, что с помощью стандартных физико-математических расчетов и методов можно достаточно правдоподобно сегодня теоретически оценить объем облучаемых мягких тканей при любых терапевтических процедурах.
Например, «золотым стандартом» теоретических расчетов в медицинской физике в отсутствие точных решений УПИ считается метод статистического моделирования Монте-Карло [16]. Хотя точность его в биомедицинской оптике и является еще спорной [17], с ошибкой не более 15% он позволяет все же моделировать распределение поглощенной энергии ЛИ в любой биоткани, если известны для нее μa, μs и g.
Чтобы показать важное преимущество такого расчета в свете рассматриваемой проблемы глубины проникновения ЛИ, рассмотрим модельную задачу равномерного освещения поверхности S кожи широким лучом с исходной плотностью мощности в луче P0. Если P0 неизменна во времени (стационарная задача), то методом Монте-Карло можно, например, для модели кожи, состоящей из двух слоев (эпидермис толщиной 100 мкм и дерма, толщина которой принята полубесконечной), получить стационарное распределение поглощенной энергии ЛИ по глубине кожи под облучаемой поверхностью. Пример такого относительного распределения для ЛИ с λ = 525 нм (зеленый диапазон спектра) и оптических свойств слоев кожи, взятых из [19], дан на рис. 3. По нему можно оценить объем кожи, в котором поглотилось, например, 50 % падающей мощности ЛИ или 90 %. Обычно в медицинской физике принято оценивать изодозы поглощения для 95 % мощности. Если определить для приведенного распределения объем V95, где поглотилось 95 % всех «фотонов», проникших в кожу, то, зная S, легко вычислить эффективную глубину zэф, до которой дошла основная часть ЛИ (краевым эффектом выхода ЛИ в стороны за края S здесь пренебрегаем), по отношению:
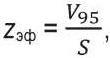 (8)
(8)
т. к. объем, занимаемый излучением, фактически имеет цилиндрическую форму. В данной задаче определенный таким образом zэф оказывается раз в 10 больше глубины ze при указанных μa, μs и g, а именно: 1,3 мм против 0,19–0,34 мм (табл.).
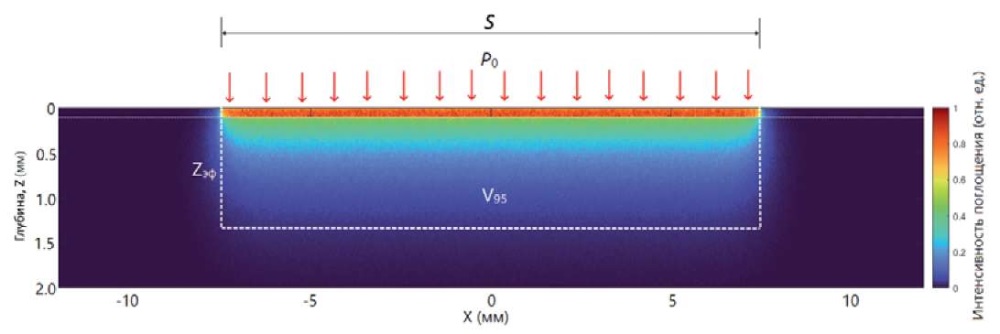
Рис. 3. Расчетное относительное распределение поглощенной энергии света
с λ = 525 нм в коже по глубине и объем V95.
Оптические параметры кожи: эпидермис µa = 7 см-¹, µs = 350 см-¹, g = 0,8;
дерма µa = 4 см-¹; µs = 220 см-¹; g = 0,8.
Падающая P0 распределена равномерно по площади освещения S
(луч, диаметром 1,5 см)
Fig. 3. Calculated relative distribution of the absorbed energy for light
with λ = 525 nm in the skin by depth and volume V95.
Skin optical parameters: µa = 7 cm-¹, µs = 350 cm-¹, g = 0,8 for epidermis;
µa = 4 cm-¹; µs = 220 cm-¹; g = 0,8 for dermis.
Incident power density P0 is distributed evenly over the illuminated area S
(beam diameter is 1.5 cm)
Аналогично на рис. 4 приведено расчетное относительное распределение поглощенной энергии для ЛИ с λ = 633 нм. Глубина zэф для красного диапазона спектра увеличилась до 3,5 мм. Увеличился и краевой эффект, но остается еще достаточно малым, чтобы его учитывать при расчете zэф в формуле (8).
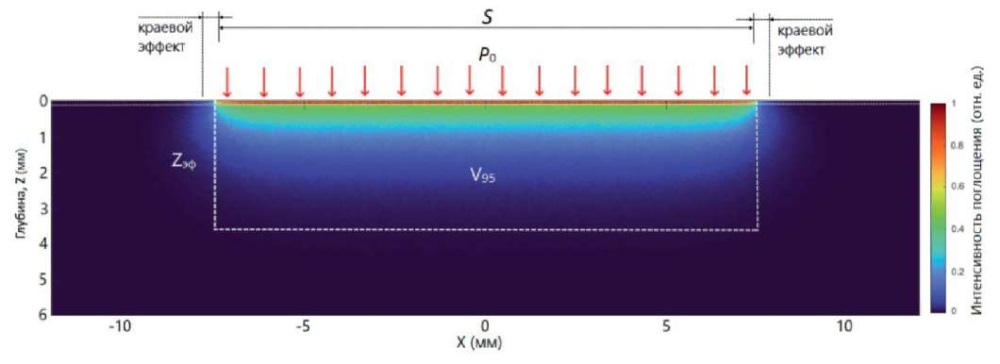
Рис. 4. Расчетное относительное распределение поглощенной энергии света
с λ = 633 нм в коже по глубине и объем V95.
Оптические параметры кожи: эпидермис µa = 3 см-¹, µs = 200 см-¹, g = 0,8;
дерма µa = 1,5 см-¹, µs = 150 см-¹, g = 0,8.
Падающая P0, аналогичная рис. 3, распределена также равномерно
по площади освещения S
Fig. 4. Calculated relative distribution of absorbed energy for light
with λ = 633 nm in the skin by depth and volume V95.
Skin optical parameters: µa = 3 cm-¹, µs = 200 cm-¹, g = 0,8 for epidermis;
µa = 1.5 cm-¹, µs = 150 cm-¹, g = 0,8 for dermis.
P0 is distributed evenly over the illuminated area S similar to Fig. 3
Безусловно, распределение поглощенной энергии по глубине в приведенных примерах будет неравномерным, спадающим по экспоненте, но это уже детали. Важно то, что мы можем в любой момент определить объем V95 и соответствующую ему глубину zэф, а отношение P0/zэф примерно при учете доли R вышедшего назад из биоткани обратнорассеянного излучения (обычно R = 0,1…0,4 [3][7], и она достаточно точно автоматически вычисляется в методе Монте-Карло) даст среднюю поглощенную и удельную по объему облучаемой биоткани мощность ЛИ:
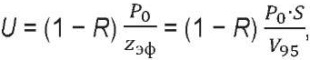 (9)
(9)
где U – поглощенная объемная плотность мощности в ткани [мВт/см³].
Кто-то может возразить, что и 5 % оставшейся мощности (скажем, 5 мВт от 100 мВт) еще достаточно для лечебного эффекта. Возможно. Это зависит в каждом конкретном случае от задействованного и рассматриваемого механизма лечебного действия (обычный нагрев, фотосупрессия при УФ-терапии, светокислородный эффект при ФДТ и т. д.). Для каждого из механизмов, кроме плацебо, существует, наиболее вероятно, своя минимальная U, которая его инициирует (аналог минимальной терапевтической дозы фармпрепарата) [3][23 и др.]. Но мы ее величину пока не знаем и здесь не обсуждаем. Мы говорим лишь, что можно определить объем V%. При необходимости можно вычислить объем для 96% поглощенной энергии, для 98% и т.д., вплоть почти до 100 %2. Основная идея здесь – возможность определения глубины воздействия через объем, в котором поглощается основная часть ЛИ. Использование zэф в качестве глубины проникновения, на наш взгляд, с практической точки зрения более аргументировано, чем ze. В частности, при теоретических оценках величина zэф оказывается больше ze, что ближе к экспериментальным данным, известным из практики. Например, для чисто поглощающей среды (μs = 0) легко получить, что zэф ≈ 3ze.
ОБСУЖДЕНИЕ И ЗАКЛЮЧЕНИЕ
Предложенный подход позволяет по-новому взглянуть на проблему глубины проникновения ЛИ при лечебных и диагностических процедурах и показать, почему часто на практике свет проникает в ткани намного глубже классической «глубины проникновения». Этот подход не вводит в оборот никаких принципиально новых терминов и определений, но позволяет получить более обоснованную с практической точки зрения теоретическую оценку глубины проникновения ЛИ в ткани, основанную на эффекте действия ЛИ, на объеме, в котором оно сосредотачивается в тканях, как при диагностике, так и в процессе терапии. В результате возникает интересный и неожиданный новый ракурс взгляда на проблему, возможно, пригодный для последующей оптимизации терапевтических процедур.
Можно, конечно, возразить, что в приведенных числовых расчетах использованы лишь частные случаи оптических свойств тканей μa, μs и g. Безусловно, это так. Но приведенные в статье конкретные числовые значения и примеры и не претендуют на большую точность и единственность возможного. Это, скорее, оценочные и демонстрационные примеры. Точные значения оптических свойств тканей наиболее правильно получать путем их измерений индивидуально у пациента перед назначением процедур. Но такие измерения требуют разработки стандартизованной методики измерений и метрологически аттестованной аппаратуры. Пока же здесь приведены лишь правдоподобные ситуации с определенной долей погрешности, которые показательны, но исключительно в методическом плане. Далее результаты могут и должны уточняться и дополняться.
Конфликт интересов:
Авторы заявляют об отсутствии конфликта интересов.
Conflict of interest:
The authors declare no conflict of interest.
1. Правомерно поставить вопрос, конечно, и о корректности оценки величин μa и μs. Есть сегодня много литературных данных, что в теоретических расчетах часто используются их завышенные значения [20][21]. Но общепринятый подход к теоретическому определению самого понятия глубины проникновения ЛИ в ткани и органы это не отменяет.
2. Точно 100 % определить нельзя, т. к. один или несколько «фотонов» могут «улететь» при статистическом моделировании далеко вглубь или в сторону от основной массы поглощенных фотонов так, что получится «пробел» в поглощении, и усреднение его по объему не будет адекватным. Наиболее достоверно методом Монте-Карло можно определять объем только до 98–99 % поглощения.
Список литературы
1. Москвин С.В. Основы лазерной терапии. Серия «Эффективная лазерная терапия» – М. – Тверь: ООО «Издательство «Триада», 2016; 1: 30–235.
2. Chung H., Dai T., Sharma S.K. et al. The nuts and bolts of low-level laser (light) therapy. Ann Biomed Eng. 2012; 40 (2): 516–533.
3. Жорина Л.В., Змиевской Г.Н. Основы взаимодействия физических полей с биологическими объектами: Воздействие ионизирующего и оптического излучения: Учебное пособие// Под ред. С.И. Щукина. – М.: МГТУ им. Н.Э. Баумана, 2006: 191–206.
4. Рогаткин Д.А. Биодозиметрический винегрет или история восприятия одной публикации в «Л-И» // Информационный бюллетень Лазерной ассоциации «Лазер-Информ». 2008; 23 (398): 14–16.
5. Загускин С.Л. Лазерная терапия – мифы и реальность, возможные пути развития // Информационный бюллетень Лазерной ассоциации «Лазер-Информ». 1999; 2 (161): 1–6.
6. Загускин С.Л., Загускина С.С. Лазерная и биоуправляемая квантовая терапия – М.: Ассоциация «Квантовая медицина», 2005: 61–159.
7. Дунаев А.В., Евстигнеев А.Р., Шалобаев Е.В. Лазерные терапевтические устройства// Под ред. К.В. Подмастерьева: Учебное пособие. – Орел: ОрелГТУ, 2005: 15–25.
8. Москвин С.В. О некоторых заблуждениях, мешающих развитию лазерной терапии. Уральский медицинский журнал. 2013; 1: 119–121.
9. Гейниц А.В., Москвин С.В., Ачилов А.А. Внутривенное лазерное облучение крови М.–Тверь: ООО «Издательство «Триада», 2012: 32.
10. Дуплик А.Ю. Дозиметрия низкоинтенсивного лазерного облучения крови. Laser Market. 1995; 2–3: 18–20.
11. Пономарев И.В. Основы использования лазеров в эстетической медицине. Вестник эстетической медицины. 2007; 1: 46–52.
12. Демин В.В., Половцев И.Г. Фотометрия и ее применения. Учебное пособие. Томск, изд-во ТГУ, 2017: 344.
13. Физический энциклопедический словарь // Под ред. акад. А.М. Прохорова – М.: Сов. энциклопедия, 1984.
14. Lister T., Wright P.A., Chappell P.H. Optical properties of human skin. J. Biomed. Opt. 2012; 17 (9): 090901.
15. Shimojo Yu et al. Measurement of absorption and reduced scattering coeffi cients in Asian human epidermis, dermis, and subcutaneous fat tissues in the 400- to 1100-nm wavelength range for optical penetration depth and energy deposition analysis. J. Biomed. Opt. 2020; 25 (4): 045002.
16. Пушкарева А.Е. Методы математического моделирования в оптике биоткани. Учебное пособие. – СПб: СПбГУ ИТМО, 2008; 103.
17. Tarasov A.P., Persheyev S., Rogatkin D.A. Analysis of the applicability of the classical probabilistic parameters of the Monte Carlo algorithm for problems of light transport in turbid biological media with continuous absorption and discrete scattering. Quantum Electron. 2021; 51 (5): 408.
18. Bikmulina P. et al. Photobiomodulation in 3D tissue engineering. J. Biomed. Opt. 2022; 27(9): 090901.
19. Salomatina E.V. et al. Optical properties of normal and cancerous human skin in the visible and near-infrared spectral range. J. Biomed. Opt. 2006; 11 (6): 064026.
20. Setchfi eld K. et al. Relevance and utility of the in-vivo and exvivo optical properties of the skin reported in the literature: a review. Biomed. Opt. Express. 2023; 14: 3555–3583.
21. Tarasov A.P., Shtyfl yuk M.E., Rogatkin D.A. Theoretical substantiation of the possibility of performing non-damaging UV diagnostics of biological tissues in vivo. Photonics. 2023; 10: 1289.
22. Rogatkin D.A., Dunaev A.V., Lapaeva L.G. Metrological support of methods and devices for non-invasive medical spectrophotometry. Biomed Eng. 2010; 44 (2): 66–70.
23. Поддубная О. А. Низкоинтенсивная лазеротерапия в клинической практике (Часть 1). Вестник восстановительной медицины. 2020; 6 (100): 92–99.
Об авторах
Д. А. РогаткинРоссия
Рогаткин Дмитрий Алексеевич – доктор технических наук, заведующий лабораторией медико-физических исследований
Москва
А. П. Тарасов
Россия
Тарасов Андрей Петрович – кандидат физико-математических наук, научный сотрудник лаборатории медико-физических исследований
Москва
М. Е. Штыфлюк
Россия
Штыфлюк Мария Евгеньевна – младший научный сотрудник лаборатории медико-физических исследований
Москва
Рецензия
Для цитирования:
Рогаткин Д.А., Тарасов А.П., Штыфлюк М.Е. Методические замечания о физических параметрах низкоинтенсивного лазерного воздействия. Часть 1. Глубина проникновения лазерного излучения. Лазерная медицина. 2023;27(4):8-15. https://doi.org/10.37895/2071-8004-2023-27-4-8-15
For citation:
Rogatkin D.A., Tarasov A.P., Shtyflyuk M.E. Methodological notes on physical parameters of low-level laser irradiation. Part 1. Penetration depth of laser light. Laser Medicine. 2023;27(4):8-15. (In Russ.) https://doi.org/10.37895/2071-8004-2023-27-4-8-15
JATS XML


























